问题
解答题
已知直角坐标平面上点Q(2,0)和圆C:x2+y2=1,动点M到圆C的切线长与|MQ|的比等于常数2,求动点M的轨迹方程,说明它表示什么曲线.
答案
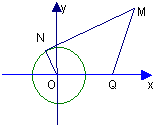
如图,设MN切圆于N,则动点M组成的集合是P={M||MN|=2|MQ|}
∵圆的半径|ON|=1
∴|MN|2=|MO|2-|ON|2=|MO|2-1
设点M的坐标为(x,y),
则
=2x2+y2-1 (x-2)2+y2
整理得3(x2+y2)-16x+17=0,即x2+y2-
x+16 3
=017 3
它表示圆心为(
,0),半径为8 3
的圆.13 3
