问题
解答题
已知△ABC中，
|
答案
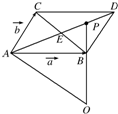
以AB、AC为邻边作▱ABDC，设对角线AD、BC交于点E，
=AE 1 2
=AD
（1 2
+a
）．b
由
=OP
+λOA
+λa
得到b
-OP
=OA
=2λ•AP
（1 2
+a
）b
=2λ
，λ∈[0，+∞），AE
∴
与AP
共线．AE
由λ∈[0，+∞）知道动点P的轨迹是射线AE，所以必过△ABC的重心．
搜题请搜索小程序“爱下问搜题”