问题
解答题
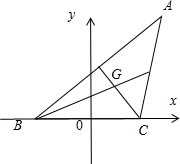
(理科做):已知:如图,△ABC的边BC长为16,AC、AB边上中线长的和为30.
求:(I)△ABC的重心G的轨迹;
(II)顶点A的轨迹方程.
答案
(I)以BC所在的直线为X轴,BC中点为原点建立直角坐标系.
设G点坐标为(x,y),
∵重心分中线比为2:1
∴|GC|+|GB|=30×
=20,2 3
根据椭圆的定义可知G点的轨迹是以B,C为焦点的椭圆,且除去轴上两点.
因a=10,c=8,有b=6,故其方程为
+x2 100
=1(y≠0)y2 36
(II)设A点坐标为(u,v)
则x=
,y=u 3
,把(3u,3v)代入G的方程得v 3
+u2 900
=1(y≠0)v2 324
故顶点A的轨迹为得
+x2 900
=1(y≠0)y2 324
