问题
单项选择题
设X1和X2是任意两个相互独立的连续型随机变量,它们的概率密度分别为f1(x)和f2(x),分布函数分别为F1(x)和F2(x),则()。
A.f1(x)+f2(x)必为某一随机变量的概率密度
B.f1(x)f2(x)必为某一随机变量的概率密度
C.F1(x)+F2(x)必为某一随机变量的分布函数
D.F1(x)F2(x)必为某一随机变量的分布函数
答案
参考答案:D
解析:
f(x)为概率密度的充要条件是: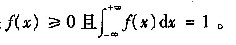
而F(x)为分布函数的充要条件是满足:①0≤F(x)≤1,F(-∞)=0,F(+∞)=1;②F(x)单调不减;③右连续。
因此只需检验上述条件是否成立即可。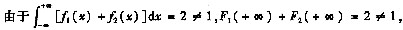
因此可先排除A,C。
又设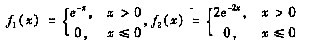
则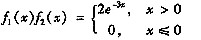
显然不满足概率密度函数的要求,进一步排除B。
