问题
单项选择题
已知三个不等式:①x2-4x+3<0,②x2-6x+8<0,③2x2-9x+m<0,要使满足①和②的所有x都满足③,则实数m的取值范围是( ).
A.(A) m>9
B.(B) m<9
C.(C) 0<m≤9
D.(D) m≤9
答案
参考答案:D
解析: 解①得1<x<3,解②得2<x<4,所以满足①和②的z的范围是2<x<3,而③的范围是
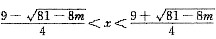 ,故应有
,故应有
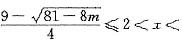
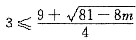 ,解得m≤9,选(D).
,解得m≤9,选(D).
已知三个不等式:①x2-4x+3<0,②x2-6x+8<0,③2x2-9x+m<0,要使满足①和②的所有x都满足③,则实数m的取值范围是( ).
A.(A) m>9
B.(B) m<9
C.(C) 0<m≤9
D.(D) m≤9
参考答案:D
解析: 解①得1<x<3,解②得2<x<4,所以满足①和②的z的范围是2<x<3,而③的范围是
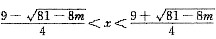 ,故应有
,故应有
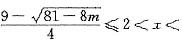
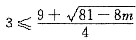 ,解得m≤9,选(D).
,解得m≤9,选(D).