问题
填空题
过原点O作圆C：x2+y2-8x=0的弦OA，则弦OA中点M的轨迹方程是______．
答案
M为OA的中点，∵∠OMC=90°，动点M在以OC为直径的圆上，
圆心坐标为：（2，0），半径为：2
∴所求点的轨迹方程为x2+y2-4x=0．
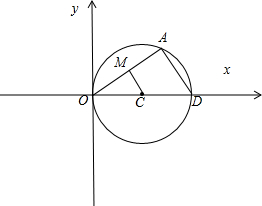
故答案为：x2+y2-4x=0．
搜题请搜索小程序“爱下问搜题”
过原点O作圆C：x2+y2-8x=0的弦OA，则弦OA中点M的轨迹方程是______．
M为OA的中点，∵∠OMC=90°，动点M在以OC为直径的圆上，
圆心坐标为：（2，0），半径为：2
∴所求点的轨迹方程为x2+y2-4x=0．
故答案为：x2+y2-4x=0．