问题
单项选择题
设f(x)在[-π，π]二阶连续可导，
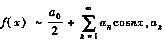是f(x)的傅氏系数，则
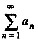
答案
参考答案：B
解析：
[分析]： [*]
为考察[*]敛散性，要对an进行估计．为此要对n。的表达式作必要的变形——分部积分．
[*]
注意|cosx|≤1，f"(x)在[-π，π]连续，故有界[*]常数M，使[*]收敛[*]收敛，即[*]绝对收敛．故应选(B)．
搜题请搜索小程序“爱下问搜题”
设f(x)在[-π，π]二阶连续可导，
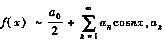是f(x)的傅氏系数，则
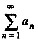
参考答案：B
解析：
[分析]： [*]
为考察[*]敛散性，要对an进行估计．为此要对n。的表达式作必要的变形——分部积分．
[*]
注意|cosx|≤1，f"(x)在[-π，π]连续，故有界[*]常数M，使[*]收敛[*]收敛，即[*]绝对收敛．故应选(B)．