问题
解答题
设△ABC的内角A,B,C所对的边分别为a,b,c,且a+c=6,b=2,cosB=
(Ⅰ)求a,c的值; (Ⅱ)求△ABC的面积. |
答案
(Ⅰ)△ABC中,a+c=6,b=2,cosB=
,则由余弦定理可得7 9
b2=4=a2+c2-2ac•cosB=a2+c2-
=(a+c)2-14ac 9
,∴ac=9.32ac 9
解得a=c=3.
(Ⅱ)△ABC的面积为
ac•sinB=1 2
×9×1 2
=21- 49 81
.2

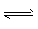 B(g)+C(g),在其它条件不变情况下,再充入一定量的A气体,A的转化率将增大。
B(g)+C(g),在其它条件不变情况下,再充入一定量的A气体,A的转化率将增大。 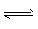 2NH3(g),增大氮气浓度可增加活化分子百分数,从而使反应速率增加。
2NH3(g),增大氮气浓度可增加活化分子百分数,从而使反应速率增加。