问题
选择题
已知函数f(x)满足f(x)=x2-2(a+2)x+a2,g(x)=-x2+2(a-2)x-a2+8.设H1(x)=max{f(x),g(x)},H2(x)=min{f(x),g(x)}(max(p,q)表示p,q中的较大值,min(p,q)表示p,q中的较小值),记H1(x)的最小值为A,H2(x)的最大值为B,则A-B=( )
A.a2-2a-16
B.a2+2a-16
C.-16
D.16
答案
取a=-2,则f(x)=x2+4,g(x)=-x2-8x+4.画出它们的图象,如图所示.
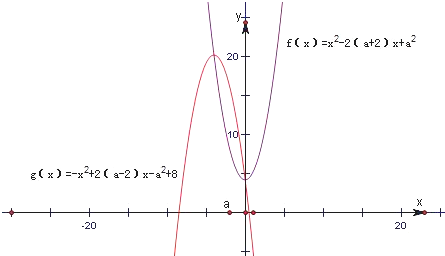
则H1(x)的最小值为两图象右边交点的纵坐标,H2(x)的最大值为两图象左边交点的纵坐标,
由x2+4=y -x2-8x+4=y
解得
或x=0 y=4
,x=-4 y=20
∴A=4,B=20,A-B=-16.
故选C.
