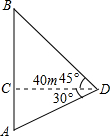问题
选择题
为了测量某塔AB的高度,在一幢与塔AB相距40m的楼顶处测得塔底A的俯角为30°,测得塔顶B的仰角为45°,那么塔AB的高度是(单位:m)( )
|
答案
根据题意画出图形,得∠BDC=45°,∠ADC=30°,DC⊥AB,DC=40m,
在Rt△BCD中,∠BDC=45°,∠BCD=90°,DC=40m,
∴BD=
=40DC cos45°
m,2
在△ABD中,∠ADB=75°,∠A=60°,BD=40
m,2
∵sin75°=sin(45°+30°)=sin45°cos30°+cos45°sin30°=
,
+6 2 4
由正弦定理
=BD sinA
得:AB=AB sin∠ADB
=BDsin∠ADB sinA
=40(1+40
×(2
+6
)2 4× 3 2
)m.3 3
故选C