问题
填空题
梯形ABCD中,若∠A:∠B:∠C=2:2:1,则∠D=______.
答案
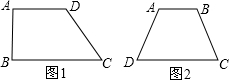
∵四边形ABCD是梯形,∠A:∠B:∠C=2:2:1,
设∠A=∠B=2x°,∠C=x°,
①若AD∥BC,
则∠A+∠B=180°,
∴2x+2x=180,
解得:x=45,
即∠A=∠B=90°,∠C=45°,
∴∠D=135°;
②若AB∥CD,
则∠B+∠C=180°,
∴2x+x=180,
解得:x=60,
即∠A=∠B=120°,∠C=60°,
∴∠D=∠C=60°;
∴∠D=60°或∠D=135°.
故答案为:60°或135°.
