参考答案：B

解析：

本题考查的是算法的时间复杂度的基本计算。

T(n)=2T(n/2)+n其实是在给n个元素进行快速排序时的最好情况下的时间递推关系式，其中T(n/2)是一个子表需要的处理时间，n为当次分割需要的时间。对此表达式变形得：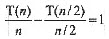

用n/2代替上式中的n有：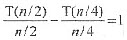

依次替换到最后是：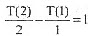

算法共需要[1og₂n]+1次分割，将替换得到的[1og₂n]+1个式子相加，最终得到：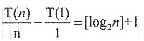

将T(1)=1代入得：T(n)=n[log₂n]+2n

因为O(n)＜O(nlog₂n)，而且对数的底可省略或为任意常数，所以：T(n)=O(nlogn)=O(nlg₁₀n)=O(nlgn)。