问题
填空题
设P是60°的二面角α-l-β内一点,PA⊥α,PB⊥β,A、B分别为垂足,PA=2,PB=4,则AB的长是 ______.
答案
如图所示,PA与PB确定平面γ,与l交于点E,则BE⊥l,AE⊥l,∴∠BEA即为二面角的平面角,∴∠BEA=60°,从而∠BPA=120°,
∴AB=PA2+PB2-2PA•PBcos∠BPA
=
=24+16+8
.7
故答案为:27
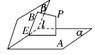
设P是60°的二面角α-l-β内一点,PA⊥α,PB⊥β,A、B分别为垂足,PA=2,PB=4,则AB的长是 ______.
如图所示,PA与PB确定平面γ,与l交于点E,则BE⊥l,AE⊥l,∴∠BEA即为二面角的平面角,∴∠BEA=60°,从而∠BPA=120°,
∴AB=PA2+PB2-2PA•PBcos∠BPA
=
=24+16+8
.7
故答案为:27
