问题
单项选择题
当窝x→0时，函数f(x)＝
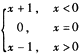的极限为( )。
答案
参考答案：D
解析： 因为[*]f(x)=[*](x+1)＝1
[*]f(x)=[*](x-1)=-1
即：[*]f(x)≠[*]f(x)，所以，当x→0时，f(x)的极限不存在，故选(D) 。
搜题请搜索小程序“爱下问搜题”
当窝x→0时，函数f(x)＝
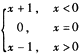的极限为( )。
参考答案：D
解析： 因为[*]f(x)=[*](x+1)＝1
[*]f(x)=[*](x-1)=-1
即：[*]f(x)≠[*]f(x)，所以，当x→0时，f(x)的极限不存在，故选(D) 。
