问题
单项选择题
曲线y=e-x2的拐点是（）。
A．(-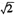
，e-2)(
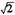，e-2)
B．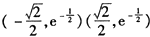
C．(-2，e-4)(2，e-4)
D．(-1，e-1)(1，e-1)
答案
参考答案：B
解析：
y'＝e-x2(-2x)，y"＝e-x2(-2x)2+e-x2(-2)＝(4x2-2)e-x2
令y"＝0，得x＝±[*]，y＝e[*]，可以验证[*]均为拐点，故选(B) 。
搜题请搜索小程序“爱下问搜题”
曲线y=e-x2的拐点是（）。
A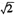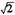．(-，e-2)(，e-2)
B．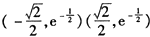
C．(-2，e-4)(2，e-4)
D．(-1，e-1)(1，e-1)
参考答案：B
解析：
y'＝e-x2(-2x)，y"＝e-x2(-2x)2+e-x2(-2)＝(4x2-2)e-x2
令y"＝0，得x＝±[*]，y＝e[*]，可以验证[*]均为拐点，故选(B) 。