问题
解答题
求证：若一梯形上底的中点到下底两个端点的距离相等，则该梯形为等腰梯形．
答案
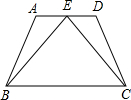
已知：在梯形ABCD中，AD∥BC，EA=ED，EB=EC．
求证：梯形ABCD为等腰梯形．
证明：
∵AD∥BC，
∴∠AEB=∠EBC，∠DEC=∠ECB．
∵EB=EC
∴∠EBC=∠ECB
∴∠AEB=∠DEC
∵EA=ED
∵△AEB≌△DEC
∴AB=DC．
又∵AD∥BC，
∴梯ABCD为等腰梯形．
搜题请搜索小程序“爱下问搜题”