问题
解答题
函数f(x)=x+
(1)当a=1时,证明:f(x)在(1,+∞)上是增函数; (2)若f(x)在(0,2)上是减函数,求a的取值范围. |
答案
证明:(1)当a=1时,f(x)=x+
(x>0,a>0),f′(x)=1-1 x
=1 x2
.…(2分)x2-1 x2
∵x>1,∴x2>1,即 x2-1>0,∴
>0,即 f′(x)>0,…(5分)x2-1 x2
∴f(x)在(1,+∞)上是增函数. …(6分)
(2)f′(x)=1-
=a x2
,…(7分)x2-a x2
使f(x)在(0,2)上是减函数,则当x∈(0,2)时,x2-a≤0恒成立,…(9分)
即a≥x2恒成立,即a≥22=4,∴a≥4. …(12分)

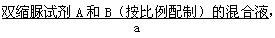 ,振荡均匀后,
,振荡均匀后, 颜色变化。
颜色变化。