已知α,β是方程4x2-4tx-1=0(t∈R)的两个不等实根,函数f(x)=
(Ⅰ)求g(t)=maxf(x)-minf(x); (Ⅱ)证明:对于ui∈(0,
|
(Ⅰ)设α≤x1<x2≤β,则4x12-4tx1-1≤0,4x22-4tx2-1≤0,∴4(
+x 21
)-4t(x1+x2)-2≤0, ∴2x1x2-t(x1+x2)-x 22
<01 2
则f(x2)-f(x1)=
-2x2-t
+1x 22
=2x1-t
+1x 21 (x2-x1)[t(x1+x2)-2x1x2+2] (
+1)(x 22
+1)x 21
又t(x1+x2)-2x1x2+2>t(x1+x2)-2x1x2+
>0 ∴f(x2)-f(x1)>01 2
故f(x)在区间[α,β]上是增函数.(3分)
∵α+β=t, αβ=-
,∴g(t)=maxf(x)-minf(x)=f(β)-f(α)=1 4
=(β-α)[t(α+β)-2αβ+2] α2β2+α2+β2+1
=
(t2+t2+1
)5 2 t2+ 25 16
(6分)8
(2t2+5)t2+1 16t2+25
(Ⅱ)证:g(tanui)=
=
(8 cosui
+3)2 cos2ui
+916 cos2ui
≥
+24cosui16 cosui 16+9cos2ui
=2 16×24 16+9cos2ui
(i=1,2,3)(9分)∴16 6 16+9cos2ui 3 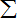
i=1
≤1 g(tanui) 1 16 6
(16+9cos2ui)=3 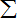
i=1
(16×3+9×3-9)1 16 6
sin2ui)(15分)∵3 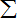
i=1
sinui=1,且ui∈(0,3 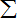
i=1
), i=1,2,3 ∴3π 2
sin2ui≥(3 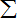
i=1
sinui)2=1,而均值不等式与柯西不等式中,等号不能同时成立,∴3 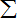
i=1
+1 g(tanu1)
+1 g(tanu2)
<1 g(tanu3) 3 4
.(14分)6
