问题
单项选择题
下列结论不正确的是
A．若已知y'=P(x)+Q(x)y+R(x)y2的一个特解，则必定可将该方程化为伯努利方程．
B．若微分方程P(x，y)dx+Q(x，y)dy=0有积分因子μ(x，y)，则μ(x，y)必定满足
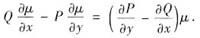
C．若函数
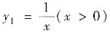是微分方程y'+y2=0的解，则y=Cy1也是该方程的解．
D．方程y"-y'2+2y=0的任何积分曲线在下半平面内不能有拐点．
答案
参考答案：C
解析：
[分析]： 对于(A)：设y*是微分方程
y'=P(x)+Q(x)y+R(x)y2
的一个特解．令y=z+y*，代入方程化简得
z'=[Q(x)+2R(x)y*]z+R(x)z2，
这正是伯努利方程，故(A)正确．
对于(B)：函数μ=μ(x，y)是微分方程Pdx+Qdy=0的积分因子的充分必要条件是
[*]
即 [*]．故(B)正确．
对于(C)：显然[*]不满足方程y'+y2=0，故(C)不正确．
对于(D)：用反证法．假设下半平面(y＜0)的点(x0，y0)是积分曲线的拐点，则y"(x0)=0，于是
[*]
与题设条件矛盾．故(D)正确．
综上分析，应选(C)．