问题
问答题
设方程p2x2+q2x+r2=0的两根分别是方程px2+qx+r=0(p≠0)的两根的平方,证明:p,q,r成等比数列。
答案
参考答案:
设方程px2+qx+r=0的两根为x1,x2,则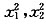 是方程p2x2+q2x+r2=0的两个根,故有
是方程p2x2+q2x+r2=0的两个根,故有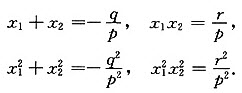
由此可得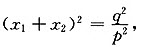 即
即
化简得q2=rp.
因q=0时,p≠0,必有r=0,原方程化为px2=0.此时方程仅有零根,与题意不符,因
此q≠0.故可知p,q,r成等比数列.
设方程p2x2+q2x+r2=0的两根分别是方程px2+qx+r=0(p≠0)的两根的平方,证明:p,q,r成等比数列。
参考答案:
设方程px2+qx+r=0的两根为x1,x2,则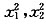 是方程p2x2+q2x+r2=0的两个根,故有
是方程p2x2+q2x+r2=0的两个根,故有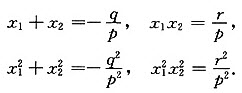
由此可得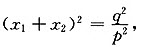 即
即
化简得q2=rp.
因q=0时,p≠0,必有r=0,原方程化为px2=0.此时方程仅有零根,与题意不符,因
此q≠0.故可知p,q,r成等比数列.