问题
填空题
三角形的两边长分别为1,
|
答案
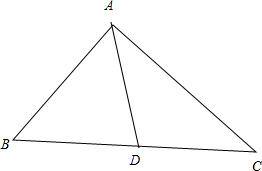
设AB=1,AC=
,AD=1,D为BC边的中点,BC=2x,3
则BD=DC=x,
△ABD中,由余弦定理可得cos∠ADB=
,12+x2-12 2x
△ADC中,由余弦定理可得,cos∠ADC=
,12+x2-(
)23 2x
因为cos∠ADB=-cos∠ADC
所以
=-12+x2-12 2x 12+x2-(
)23 2x
∴x=1
∴BC=2
∴AB2+AC2=BC2即A=90°
∴外接圆的直径2R=BC=2,从而可得R=1
故答案为:1.