问题
解答题
证明:等腰梯形在同一底上的两角相等(要求写出已知,求证,证明并画出图形).
答案
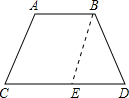
已知:梯形ABCD中,AB∥CD,AC=BD,
求证:(1)∠A=∠ABD,(2)∠C=∠D,
证明:(1)过B作BE∥AC交CD于E,
又∵AB∥CD,
∴四边形ACEB是平行四边形,
∴AC=BE,
∵AC=BD,
∴BE=BD,
∴∠BED=∠D,
∵AC∥BE,
∴∠C=∠BED,
∴∠C=∠D,
(2)∵AB∥CD,
∴∠A+∠C=180°,∠D+∠ABD=180°,
∵∠C=∠D,
∴∠A=∠ABD.