问题
解答题
| 已知直线l1:y=x和直线l2:y=-x,动点M到x轴的距离小于到y轴的距离,且M到l1,l2的距离之积为常数4. (1)求动点M的轨迹C的方程; (2)过点N(3,0)的直线L与曲线C交与P、Q,若
|
答案
(1)由题意
•|x-y| 2
=4且|x|>|y|,|x+y| 2
∴x2-y2=8 …(5分)
(2)设P(x1,y1),Q(x2,y2),易知直线倾斜角不为0,可设直线L方程为 x=ty+3
代入双曲线方程得:(t2-1)y2+6ty+1=0,△>0
y1+y2=
,y1y2=-6t t2-1
(1)1 t2-1
又
=2PN
则y1=-2y2 (2)NQ
联立(1)(2)得:t=±1 73
所以直线L方程为:
x±y-73
=0 …(12分)73

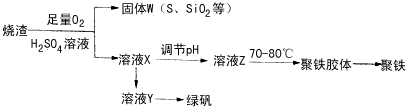
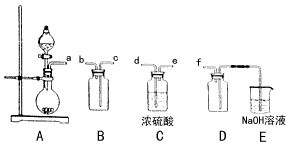
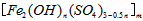 ,广泛用于污水处理。实验室利用硫酸厂烧渣(主要成分为铁的氧化物及少量FeS、SiO2等)制备聚铁和绿矾(FeSO4·7H2O )过程如下
,广泛用于污水处理。实验室利用硫酸厂烧渣(主要成分为铁的氧化物及少量FeS、SiO2等)制备聚铁和绿矾(FeSO4·7H2O )过程如下