（Ⅰ）当a=2时，f（x）=x|x-2|=

x(x-2)，x≥2 x(2-x)，x＜2

由二次函数的性质知，单调递增区间为（-∞，1]，[2，+∞）（开区间不扣分）

（Ⅱ）因为a＞2，x∈[1，2]时，所以f（x）=x（a-x）=-x²+ax=-(x-

a

2

)2+

a2

4

当1＜

a

2

≤

3

2

，即2＜a≤3时，f（x）_min=f（2）=2a-4

当

a

2

＞

3

2

，即a＞3时，f（x）_min=f（1）=a-1

∴f(x)min=

2a-4，2＜a≤3 a-1，a＞3

（Ⅲ）f(x)=

x(x-a)，x≥a x(a-x)，x＜a

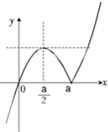
①当a＞0时，图象如上图左所示

由

y= a2 4 y=x(x-a)

得x=

( 2 +1)a

2

∴0≤m＜

a

2

，a＜n≤

2 +1

2

a

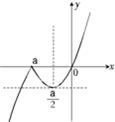
②当a＜0时，图象如上图右所示

由

y=- a2 4 y=x(a-x)

得x=

(1+ 2)

2

a

∴

1+ 2

2

a≤m＜a，

a

2

＜n≤0