问题
单项选择题
设函数f(x)在区间(0,+∞)上可导,且
 求函数F(x)的单调区间,并求函数y=F(x)的图形的凹凸区间及拐点.
求函数F(x)的单调区间,并求函数y=F(x)的图形的凹凸区间及拐点.
答案
参考答案:[解] [*]
[*]
又F'(1)=0,所以F(x)在区间(0,+∞)上严格单调增加.
[*]
所以当0<x<1时,F"(x)<0,曲线y=F(x)为凸;当1<x<+∞时,F"(x)>0,曲线y=F(x)为凹,F(1)=0,所以点(1,0)是曲线y=F(x)的拐点.
解析:[评注] 为了弄清楚
[*]的符号,将等式右边的第二、第三两项合并改写为
[*]
然后将F'(x)的表达式写成一个积分
[*]
这样可以方便地看出F'(x)的符号.这种处理方法是解决本题的关键,请读者注意学习.

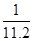 mol·L-1、w=
mol·L-1、w=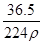 %
% mol·L-1、w=
mol·L-1、w=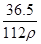 %
% %
%