问题
单项选择题
设f(0)=0，则f(x)在点x=0可导的充要条件为[ ]
答案
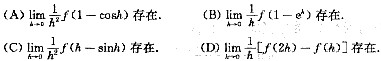
参考答案：B
解析：方法1 考虑必要性．设f'(0)存在，分别将(A)～(D)凑成f'(0)的定义式．
(A)[*]在前一式中命1-cosh=x，从而有，当h→0时x→0+，有
[*]所以(A)存在．
(B)[*]在前一式中命1-eh=x，从[*]
[*]所以(B)存在．
(C)[*]前一式中命h-sinh=x，从而当h→O时x→0，有
[*]
=f'(0)×0=0．
所以(C)存在．
[*]
所以(D)存在．
所以(A)～(D)为f'(0)存在的必要条件．
反之，只有(B)是f'(0)存在的充分条件．事实上，设(B)成立，记其极限为B，则
[*]
所以f'(0)存在．
至于(A)，由以上讨论可见，由(A)存在，只能推知f'+(0)存在，(A)不充分．
至于(C)，设(C)成立，记其极限为C，于是
[*]
而[*]
所以由[*]存在，不知道[*]是否存在．(C)不充分．
至于(D)，由
[*]
存在，推不出由它拆开的两个极限
[*]
分别存在，所以(D)不充分．
方法2 举例说明(A)、(C)、(D)不充分．
(A)的例子．设f'(x)=|x|，有f(0)=0，则
[*](存在)，但f(x)=|x|在x=0处不可导．所以(A)不充分．
(C)的例子．设[*]有f(0)=0，则
[*]
但[*]在x=0处不可导．
(D)的例子．设[*]有f(0)=0，
[*]
但f(x)在x=0处不可导．
以上说明(A)、(C)、(D)都不充分，当然谈不上充要了．