问题
单项选择题
设g(x)在x=0处存在二阶导数,且g(0)=1,g'(0)=2,g"(0)=1,并设
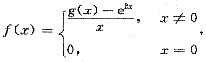
求f'(0),并讨论f'(x)在x=0处的连续性.
答案
参考答案:[解] 当x≠0时,有
[*]
而[*]
因为g'(x)在x=0处连续,所以[*]式(2.1)为[*]但题中未设在x=0的某邻域当x≠0时g"(x)存在,故式(2.1)不能再用洛必达法则,此时应采用凑成导数的形式去求极限,现在实际上要去凑成g"(0)的形式:
[*]
[*]
再计算
[*]
所以f'(x)在x=0处连续.
解析:[评注] 对于[*]如果条件中仅设f'(x0)与g'(x0)存在,而未设在x=x0的去心邻域内f'(x)与g'(x)存在,那么不能用洛必达法则,而应采用凑成导数的形式(如式(2.2)).
