问题
单项选择题
设y=y(x)是由方程y3+xy+x2-2x+1=0确定并且满足y(1)=0的连续函数,则
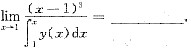
答案
参考答案:[解] 应填-3.
[*]
由隐函数求导,有
[*]
得
[*]
有
[*]
对式(2.10)再用洛必达法则:
[*]
将式(2.11)对x再求导,有
[*]
x→1时已知y(x)→0,y'(x)→0.经计算y"(x)→-2.于是
[*]
解析:[评注] 求隐函数的导数时,常常是给出x=x0,要求y'(x0)= 此时,一般应从F(x,y)=0中计算出当x=x0时y= 代入已计算出的y'(x)便得y'(x0).在求y"(x)时,都应将y'(x)中的y看成x的函数求之,如式(2.12)那样.
