问题
解答题
2006年8月中旬，湖南省资兴市遇到了百年不遇的洪水灾害。在资兴市的东江湖岸边的O点处（可视湖岸为直线）停放着一只救人的小船，由于缆绳突然断开，小船被风刮跑，其方向与湖岸成15°，速度为2.5km/h，同时岸上一人，从同一地点开始追赶小船，已知他在岸上追的速度为4 km/h，在水中游的速度为2 km/h，问此人能否追上小船？若小船速度改变，则小船能被此人追上的最大速度是多少
答案
能追上小船，小船能被人追上的最大速度是2
km/h
如图，设此人在岸上跑到A点后下水，在B处追上小船
设船速为v，人追上船的时间为t，人在岸上追船的时间
为t的k倍（0＜k＜1），则人在水中游的时间为（1－k）t
故｜OA｜＝4kt，｜AB｜＝2（1－k）t，｜OB｜＝vt
由余弦定理得：
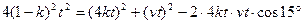
整理得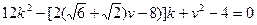
要使方程在0＜k＜1内有解，则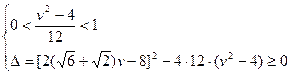
解得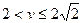 
，即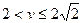时，人可以追上船
故船速为2.5km/h时，能追上小船，小船能被人追上的最大速度是2km/h