问题
单项选择题
如图，已知△ABC的面积为54平方厘米，D、E、F分别是BC、AB、EC上的点，如果CF:CE=a，CD:CB=b，BE:BA=c，且0＜a、b、c＜1，a+b+c=1，则△DCF面积的最大值是()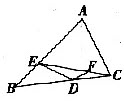
A．2平方厘米
B．3平方厘米
C．9平方厘米
D．18平方厘米
答案
参考答案：A
解析：
等高三角形的面积比就是底边比。S△BEC=cS△ABC，S△DEC=bS△BEC，S△DCF=aS△DEC，所以S△DCF=abcS△ABC。因为a+b+c=1，所以当时，△DCF的面积最大，为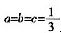
平方厘米。