问题
问答题
设一个直角三角形的三边成等差数列,最短直角边等于3.若方程x2-(k+2)x+k+7=0的两根的平方和等于该直角三角形斜边的平方,求k的值。
答案
参考答案:
设直角三角形的另一直角边为6,斜边为c,则3,b,c为等差数列.故2b=3+c,
又:c2=32+b2,
由此解得b=4,c=5.
若方程x2=(k+2)x+k+7=0的两根为x1,x2,则x1+x2=k+2,x1x2=k+7,所以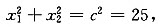
即(x1+x2)2-2x1x2=(k+2)2-2(k+7)=25,
化简得k2+2k-35=0,
解得k=-7或k=5.
