问题
单项选择题
设函数z=f(x，y)在点(x0，y0)处有f'x(x0，y0)=a，f'y(x0，y0)=b，则
A．极限
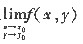一定存在，但f(x，y)在点(x0，y0)处不连续．
B．f(x，y)在点(x0，y0)处必连续．
C．dz|(x0，y0)=adx+bdy．
D．
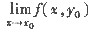及
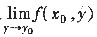存在且相等．
答案
参考答案：D
解析：
[分析]： 由f'x(x0，y0)存在即知一元函数f(x，y0)在x=x0处连续，故[*]．类似由f'y(x0，y0)存在即知一元函数f(x0，y)在y=y0处连续，故[*]．即(D)正确．
或举反例用排除法．取[*]，计算可得f'x(0，0)=f'y(0，0)=0，同时可证明[*]存在，f(x，y)在点(0，0)处连续，f(x，y)在点(0，0)处不可微分，这样可排除(A)，(C)．
取[*]计算可得f'x(0，0)=f'y(0，0)=0，同时可证明f(x，y)在点(0，0)处不连续，这样可排除(B)．由排除法可知，应选(D)．