问题
单项选择题
设可导函数x=x(t)由方程
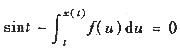所确定，其中可导函数f(u)＞0，且f(0)=f'(0)=1，则x"(0)=
答案
参考答案：C
解析：
[分析]： 令t=0，由题设方程可得x(0)=0．在题设方程两边对t求导，得
cost-f[x(t)]x'(t)+f(t)=0， (*)
在(*)式中令t=0，可得x'(0)=2．在(*)两边再对t求导，得
-sint-f'[x(t)][x'(t)]2-f[x(t)]x"(t)+f'(t)=0， (**)
在(**)式中令t=0，可得x"(0)=-3．故选(C)．