问题
单项选择题
设函数F(x,y,z)具有连续偏导数,若从方程F(x,y,z)=0能分别解出函数x=f(y,z),y=g(z,x)与z=h(x,y),则未必有
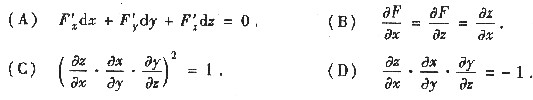
答案
参考答案:B
解析:[分析一] 把F(x,y,z)=0看成关于(x,y)的恒等式,并将恒等式两边求微分,由一阶全微分形式不变性即得
F'xdx+F'ydy+F'zdz=0. (*)
从而不选(A).
由(*)式可得[*],从而
[*]
计算可得
[*]
从而也不选(C)与(D).即应选(B).
[分析二] 用举例法即可选出正确选项.考虑函数F(x,y,z)=x+y+z,于是F'x=1,f'z=1,又由z=-(x+y)知z'x=-1.这表明F'x=F'z≠z'x.应选(B).
