问题
单项选择题
设
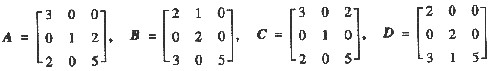，那么与对角矩阵相似的矩阵是
答案
参考答案：B
解析：
[分析]： 矩阵A的特征值是1，3，5，因为矩阵A有三个不同的特征值，所以A～Λ．
矩阵B的特征值是2，2，5，由于秩
[*]
所以，λ=2只有一个线性无关的特征向量，因而矩阵曰不能相似对角化．
矩阵C是实对称矩阵，故必有C～Λ．
矩阵D的特征值也是2，2，5，由于
[*]
所以，λ=2有两个线性无关的特征向量，因而矩阵D可以相似对角化．故应选(B)．
评注 本题归纳了判断相似对角化的基本思路与方法．当AT=A或A有n个不同的特征值时，矩阵A必可相似对角化；而当特征值有重根时，要通过秩来判断．
