问题
解答题
已知:关于x的一元二次方程ax2+2(a-3)x+a+3=0有两个实数根,且a为非负整数。
(1)求a的值;
(2)若抛物线y=ax2+2(a-3)x+a+3向下平移m(m>0)个单位后过点 (1,n) 和点(2,2n+1),求m的值;
(3)若抛物线y=ax2+2(a-3)x+a+3上存在两个不同的点P、Q关于原点对称,求k的取值范围。
答案
解:(1)依题意,得△=[2(a-3)]2-4a(a+3)=-36a+36≥0,
解得a≤1,
又a≠0且a为非负整数,
∴a=1,
∴y=x2-4x+4;
(2)抛物线y=x2-4x+4过点(1,1),(2,0),向下平移m(m>0)个单位后得到点(1,n)和点(2,2n+1),
∴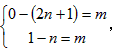
解得m=3;
(3)设P(x0,y0),则Q(-x0,-y0),
∵P、Q在抛物线y=x2-4x+4+k上,
将P、Q两点坐标分别代入得: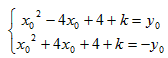 ,
,
将两方程相加得:2x02+8+2k=0,即x02+4+k=0,
∵△′=-4(4+k)≥0,
∴k≤-4,
当k=-4时,P、Q两点重合,不合题意舍去,
∴k<-4。
