问题
选择题
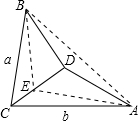
将Rt△ABC沿直角的角平分线CD折成直二面角(平面ACD⊥平面BCD),则∠ACB的度数是( )
A.90°
B.60°
C.45°
D.由直角边的长短决定
答案
过B作BE⊥CD,由题意得到BE⊥平面ACD,
∴BE⊥AE,连接AB,可得△ABE为直角三角形,
∵折叠前,CD为∠ACB的角平分线,
∴∠BCE=∠ACE=45°,
设AC=b,BC=a,在△BCE中,BE=CE=
a,2 2
在△ACE中,由余弦定理得:AE2=b2+(
a)2-2b•2 2
a•cos45°=2 2
a2+b2-ab,1 2
根据勾股定理得:AB2=BE2+AE2=a2+b2-ab,
在△ABC中,由余弦定理得:AB2=a2+b2-2abcos∠ACB=a2+b2-ab,
∴cos∠ACB=
,∠ACB为锐角,1 2
则∠ACB=60°.
故选B