问题
单项选择题
将12个球放人3个盒子里，使每个盒子里球的数目是偶数，且没有空盒，问共有几种放法（）
A．10
B．12
C．8
D．6
答案
参考答案：A
解析：
[命题提示] 本题考查排列组合问题 [解题要点] 将12分解为三个偶数之和，再求其放入方法数 [答案与解析] 12可写为2+2+8、2+4+6、4+4+4，对于12=2+2+8，有3种放球的方法；对于12=2+4+6，有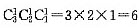
种放球的方法；对于12=2+2+8，只有1种放球的方法。所以共有3+6+1=10种放法。故选A。