已知△ABC中，AC=2
|
∵AC=b=2
，BC=a=2，2
∴由正弦定理
=a sinA
，得b sinB
=2 sinA 2 2 sinB
即sinA=
sinB2 2
∵a＜b，sinB∈（0，1]
∴sinA∈（0，
]，可得锐角A∈[2 2
，0）π 4
∵余弦函数在（0，π）内为减函数，
∴cosA的取值范围是[
，1)2 2
故选：B
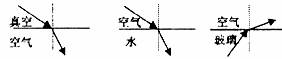
如下图所示是张鸿同学在探究光在表中列出的几种介质中发生折射时据折射现象画出的光路图。
| 介质 | 光速(m／s) |
| 真空 | 3×10 |
| 空气 | 2.99×10 |
| 水 | 2.25×10 |
| 玻璃 | 2×10 |
(2)分析表中的数据和上图所示的光路图可以得出光在折射时遵循的规律是 。（3分）
(3)由分析的结论可知，光从水中斜射入玻璃中，折射角 入射角(填“大于”或“小于”)
(4)探究到这里，张鸿同学想“光在反射现象中，光路是可逆的，那么在折射现象中，光路是否也是可逆的呢?”，为探究这一问题，请你帮她设计一个探究方案。（4分）
(5)现代医学中常用超声波击碎人体内的结石，超声波从空气中斜射入人体后也类似光一样要发生折射，如右所示，超声波进入人体击碎结石时，入射点应在0点的 (填“左侧”或“右侧”) （2分）