问题
单项选择题
由曲线x2=4y,x2=-4y,x=4,x=-4围成的图形绕y轴旋转一周所得旋转体的体积为Vl;满足x2+y2≤16,x2+(y-2)2≥4,x2+(y+2)2≥4的点(x,y)组成的图形绕y轴旋转一周所得旋转体的体积为V2,则()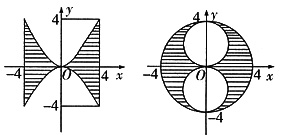
A.V1=(1/2)V2
B.V1=(2/3)V2
C.V1=V2
D.V1=2V2
答案
参考答案:C
解析:
如题图,两图形绕y轴旋转所得旋转体夹在两相距为8的平行平面之间,用任意一个与y轴垂直的平面截这两个旋转体,设截面与原点距离为|y|,则所得截面面积
S1=π(42-4|y|),
S2=π(42-y2)-π[4-(2-|y|)2]=π(42-4|y|)∴S1=S2
由祖暅原理知,两几何体体积相等,
∴V1=V2.故选C.
