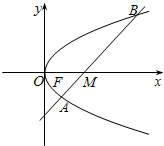问题
解答题
| 已知动圆过定点Q(1,0),且与定直线x=-1相切. (1)求此动圆圆心P的轨迹C的方程; (2)若过点M(4,0)的直线l与曲线C分别相交于A,B两点,若2
|
答案
(1)由题意知,动圆圆心M的轨迹C是以定点Q(1,0)为焦点,以定直线
x=-1为准线的抛物线,其方程为:y2=4x;
(2)设直线AB的方程为:y=k(x-4)(k存在且k≠0).
联立
,消去x,得ky2-4y-16k=0,y=k(x-4) y2=4x
显然△>0,
设A(x1,y1),B(x2,y2),
则y1+y2=
,y1y2=-16.4 k
=(4-x1,-y1),AM
=(x2-4,y2).MB
又∵2
=AM
,∴-2y1=y2.MB
联立
,消去y1,y2得k2=2,解得k=±y1+y2= 4 k y1y2=-16 -2y1=y2
.2
∴直线l的方程为y=±
(x-4).2