问题
选择题
等腰△ABC中，一腰上的高
|
答案
根据题意画出图形，如图所示：
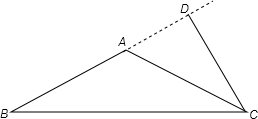
在直角三角形BCD中，
由题意知：CD=
，∠DCB=60°，AB=AC，3
∴∠B=∠ACB=30°，∴BC=2CD=2
，3
∴∠BAC=120°，
根据正弦定理得：
=2R，（R为△ABC外接圆的半径）BC sin∠BAC
R=
=2．2 3 2sin120°
故选C
搜题请搜索小程序“爱下问搜题”
等腰△ABC中，一腰上的高
|
根据题意画出图形，如图所示：
在直角三角形BCD中，
由题意知：CD=
，∠DCB=60°，AB=AC，3
∴∠B=∠ACB=30°，∴BC=2CD=2
，3
∴∠BAC=120°，
根据正弦定理得：
=2R，（R为△ABC外接圆的半径）BC sin∠BAC
R=
=2．2 3 2sin120°
故选C