问题
解答题
△ABC中内角A，B，C的对边分别为a，b，c，已知a＝bcos C＋csin B.
(1)求B；
(2)若b＝2，求△ABC面积的最大值．
答案
（1）B＝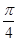
（2）
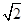＋1
(1)由已知及正弦定理，得
sin A＝sin Bcos C＋sin Csin B，①
又A＝π－(B＋C)，
故sin A＝sin(B＋C)＝sin Bcos C＋cos Bsin C．②
由①，②和C∈(0，π)得sin B＝cos B.
又B∈(0，π)，所以B＝.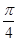
(2)△ABC的面积S＝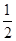
acsin B＝
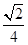ac.
由已知及余弦定理，得4＝a2＋c2－2accos.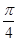
又a2＋c2≥2ac，故ac≤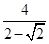
，
当且仅当a＝c时，等号成立．
因此△ABC面积的最大值为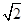＋1.