问题
填空题
已知半径为1的动圆与圆(x-5)2+(y+7)2=16相切,则动圆圆心的轨迹方程是______.
答案
圆(x-5)2+(y+7)2=16的圆心为C(5,-7),半径r=4.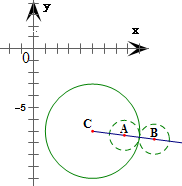
∵半径为1的动圆与圆(x-5)2+(y+7)2=16相切,
∴当两圆内切时,动圆圆心A到点C的距离等于两圆的半径之差的绝对值,
|BC|=4-1=3,因此动圆圆心的轨迹为以C为圆心,半径等于3的圆,
轨迹方程为(x-5)2+(y+7)2=9;
当两圆外切时,动圆圆心B到点C的距离等于两圆的半径之和,
|BC|=4+1=5,因此动圆圆心的轨迹为以C为圆心,半径等于5的圆,
轨迹方程为(x-5)2+(y+7)2=25.
综上所述,所求动圆圆心的轨迹方程是(x-5)2+(y+7)2=9或(x-5)2+(y+7)2=25.
故答案为:(x-5)2+(y+7)2=9或(x-5)2+(y+7)2=25.
