问题
解答题
已知关于x的方程x2-2x-2n=0有两个不相等的实数根。
(1)求n的取值范围;
(2)若n<5,且方程的两个实数根都是整数,求n的值。
答案
解:(1)∵于x的方程x2-2x-2n=0的二次项系数a=1、一次项系数b=-2、常数项c=-2n,
∴△=b2-4ac=4+8n>0,
解得,n>-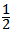 ;
;
(2)由原方程,得(x-1)2=2n+1,
∴x=1±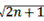 ;
;
∵方程的两个实数根都是整数,且n<5,
∴0<2n+1<11,且2n+1是完全平方形式,
∴2n+1=1,2n+1=4或2n+1=9,
解得,n=0,n=1.5或n=4。
