问题
填空题
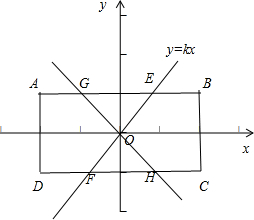
矩形ABCD的四个顶点的坐标分别为A(-2,1),B(2,1),C(2,-1),D(-2,-1),过原点且互相垂直的两条直线分别与矩形的边相交于E、F、G、H四点,则四边形EGFH的面积的最小值为______,最大值为______.
答案
设过原点且互相垂直的两条直线分别为 y=kx,和 y=-
x,(不妨设k>0)由题意得,1 k
则 E (
,1),F (-1 k
,-1),G(-k,1),H(k,-1),1 k
由两点间的距离公式得 EF=
=2(
)2+222 k
,GH=1+ 1 k2
=2(2K)2+4
,1+k2
四边形EGFH的面积为 S=
•EF•GH=21 2
=22+k2+ 1 k2
=2|k+(k+
)21 k
|=2(k+1 k
).1 k
根据E、G 两点都在线段AB上,可得-2≤
≤2,且-2≤-k≤2,∴1 k
≤k≤2.1 2
又函数 S=2(k+
) 在[1 k
,1]上是减函数,在[1,2]上是增函数,故 k=1时,S有最小值为4.1 2
当 k=
时,S=5; 当 k=2时,S=5. 当 k=0时,S=4.1 2
综上,S的最小值等于4,最大值等于 5,
故答案为 4,5.