问题
填空题
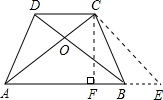
若等腰梯形ABCD的上、下底之和为4,并且两条对角线所夹锐角为60°,则该等腰梯形的面积为______.(结果保留根号的形式)
答案
已知梯形的上下底的和是4,设AB+CD=4,
对角线AC与BD交于点O,经过点C作对角线BD的平行线CE交AB的延长线于点E.
(1)当∠DOC=60度时,∠ACE=60°,△ACE是等边三角形,边长AC=CE=AE=4,
作CF⊥AE,CF=4×sin60°=4×
=23 2
;3
因而面积是
×4×21 2
=43
;3
(2)当∠BOC=60度时,∠AOB=180°-60°=120°,又BD∥CE,∴∠ACE=∠AOB=120°,
∴△ACE是等腰三角形,且底边AE=4,
因而∠CEA=
=30°,作CF⊥AE,则AF=FE=2,CF=2×tan30°=180°-120° 2
,2 3 3
则△ACE的面积是
×4×1 2
=2 3 3
.4 3 3
而△ACE的面积等于梯形ABCD的面积.
因而等腰梯形的面积为4
或3 4 3
.3