问题
填空题
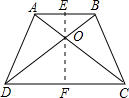
若等腰梯形ABCD的上,下底之和为2,并且两条对角线所交的锐角为60°,则等腰梯形ABCD的面积为______.
答案
分两种情况考虑:过O作OE⊥AB,反向延长交CD于F.
(i)当∠AOB=∠COD=60°
∵四边形ABCD是等腰梯形
∴OA=OB,OC=OD
∵∠AOB=∠COD=60°
∴△OAB,△OCD均是等边三角形
设AB=x,则CD=2-x
∴OE=
x,OF=3 2
(2-x)3 2
∴EF=3
∴S梯形ABCD=
(AB+CD)•EF=1 2
×2×1 2
=3
;3
(ii)当∠AOD=∠BOC=60°
∴∠AOB=∠COD=120°
∴∠OAB=∠OBA=∠ODC=∠OCD=30°
设AB=x,则CD=2-x
∴OE=
x,OF=3 6
(2-x)3 6
∴EF=OE+OF=3 3
∴S梯形ABCD=
(AB+CD)•EF=1 2
×2×1 2
=3 3 3 3
综上,等腰梯形ABCD的面积为
或3
.3 3