问题
解答题
已知关于x的方程x2-2ax-a+2b=0，其中a、b为实数。
（1）若此方程有一个根为2a（a＜0），判断a与b的大小关系并说明理由；
（2）若对于任何实数a，此方程都有实数根，求b的取值范围。
答案
解：（1）∵方程x2-2ax-a+2b=0有一个根为2a，
∴4a2-4a2-a+2b=0，
整理，得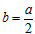
，
∵a＜0，
∴
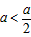，即a＜b；
（2）△=4a2-4（-a+2b）=4a2+4a-8b，
∵对于任何实数a，此方程都有实数根，
∴对于任何实数a，都有4a2+4a-8b≥0，即a2+a-2b≥0，
∴对于任何实数a，都有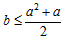
，
∵
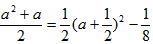
当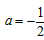
时，
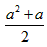有最小值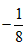
，
∴b的取值范围是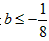
。
