问题
填空题
已知12+22+32+…+n2=
|
答案
∵12+22+32+…+n2=
n(n+1)(2n+1),1 6
∴12+22+32+…+1002=22+42+62+…+1002+(12+32+52+…+992)
×100×(100+1)(2×100+1)=338350;1 6
又∵22+42+62+…+1002-(12+32+52+…+992)
=(22-12)+(42-32)+(62-52)+…+(1002-992)
=(2+1)(2-1)+(4-3)(4+3)+(6+5)(6-5)+…+(100+99)(100-99)
=(2+1)+(4+3)+(6+5)+…+(100+99)
=5050;
∴22+42+62+…+1002=
=171700.338350+5050 2
故答案为:171700.

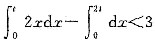 ,则t∈().
,则t∈().